Arithmetische und logische Befehle -Adressierung der Operanden
Arithmetische und logische Befehle umfassen die Grundrechenarten und boolschen Operationen der ALU. Bei RISC-Architekturen wird versucht die Länge, den Speicherplatz der Befehle gleich gross zu machen, das hat entscheidende Vorteile beim Pipelining. Die meisten AVR-Befehle haben eine Länge von 16 Bit d.h. einen 16 Bit-Op-Code (Operation-Code) damit sie mit einem Speicherzugriff geladen und möglichst in einem Takt durchgeführt werden können. In den 16 Bit muss der Operator und die Operanden kodiert werden. Es gibt Operationen, die nur einen Operanden haben (Negation, erhöhe um 1 usw.) und Operationen mit zwei Operanden (+,-, UND, ODER). Das Zielregister (Rd destination) einer Operation ist immer das erste Operanden-Quellregister. Der zweite Operand kann ein Register (Register-Adressierung) oder eine (8Bit) Konstante (Immediate-Adressierung) sein Beispiele:
- Ein Register inc R16 ;R16 := R16+1
- Zwei Register sub R16,R17 ;R16 := R16-R17
- Register mit Konstante subi R16,3 ;R16 := R16-3
Op-Code bei Register-Adressierung
| Syntax | Benennung | Operation | Operanden | 16 Bit-Op-Code |
|---|---|---|---|---|
| sub Rd, Rr | Subtract Two Working Registers | Rd:=Rd - Rr | 0 ≤ d ≤ 31, 0 ≤ r ≤ 31 | 0001 10rd dddd rrrr |
Der zweite Operand ist ein Register (Rr). Die Operanden können eines der 32 Universalregister sein. Um eines der 32 Register aus zu wählen benötigt man 5Bit 25 = 32. Damit benötigt man 2*5Bit um die beiden Register zu bestimmen, es bleiben noch 6Bit für die Bestimmung der Operation übrig.
Op-Code bei Konstanten (Immediate-) Adressierung
Immediate (engl.) bedeutet soviel wie unmittelbar, unverzüglich. Der zweite Operand steht nicht in einem Register sondern ist bereits im Befehl enthalten, das hat leider Konsequenzen:
| Syntax | Benennung | Operation | Operanden | 16 Bit-Op-Code |
|---|---|---|---|---|
| subi Rd, K8 | Subtract Constant from Working Register* | Rd:=Rd - K8 | 16 ≤ d ≤ 31, 0 ≤ K8 ≤ 255 | 0101 KKKK dddd KKKK |
Bei einem 8 Bit µC sollte ein Immediate-Operand auch 8 Bit Breite (K8) haben. Somit bleiben von den 16 Bit nur noch 8 übrig für die Kodierung des Operators und des Registers. Atmel hat sich entschieden 4 Bit für die Register-Adressierung zu verwenden (dddd), somit wurden nicht alle 32 sondern nur die oberen 16 Register für Immediate-Operationen verfügbar (beachte die * hinter den Beschreibungen im Befehlssatz). Es gibt noch eine Einschränkung -es gibt kein addi Rd,K8. Statt dessen verwendet man subi Rd,-K8.
Merke: Immediate geht nur mit Register R16..R31! Statt addi nehme man subi mit negativer Konstante!
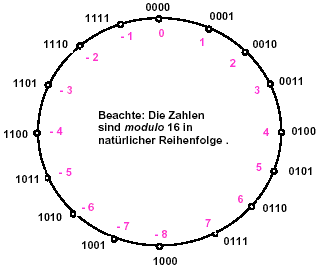
Darstellung negativer Zahlen (Zweierkomplement)
Will man auch negative Zahlen (signed) verwenden, müssen die mögichen Werte z.B. 0..255 auf positive und negative Zahlen aufgeteilt werden (-128..-1,0..127). Eine Kodierung ist besonders praktisch -das Zweierkomplement:
Prinzip für 4 Bit: Zähle von 0 aufwärts bis zu +7, dann gehts bei -8 bis zur -1 weiter.
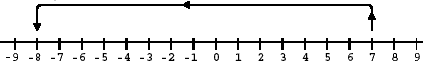 |
|||||||||||||||||
|
|
||||||||||||||||
| Wenn das vorderste Bit (MSB) = 1, ist die Zahl negativ!
Addition zweier signed Zahlen ist dann einfach. |
|||||||||||||||||
Beispiel für 4Bit: Berechne in der Zweierkomplementdarstellung 5 + (-3)
Umwandlung von -3 ins Zweierkomplement:
- Stelle 3 als Dualzahl dar: 3 = 0011
- Negiere die Bits (Einerkomplement): 1100
- Addiere 1 dazu: 1101 = -3
Lösung: 5 = 0101; -3 = 1101; 0101+1101 = 10010 =Übertrag weg wegen modulo 16=> 0010 = 2
Weitere Beispiele:
Gesucht -6: 610 = 0110 =invertieren=> 1001 + 1 = 10102
Gesucht -1; 110 = 0001 =invertieren=> 1110 +1 = 11112
Rückumwandeln einer negativen (im Zweierkomplement dargestellten) Zahl funktioniert genauso:
Gesucht: 11012 =invertieren=> 0010 + 1 = 0011 = 310
Arithmetikflags
Im Statusregister (SREG) des Prozessors gibt es eine Reihe von Flags, die durch Rechenergebnisse beeinflusst werden:
| I | T | H | S | V | N | Z | C |
|---|---|---|---|---|---|---|---|
| Interrupt | Transfer | Half Carry | Signed Tests | Two's Complement | Negative | Zero | Carry |
Carry C
10100011
+ 11110011
---------
110010110
Das Carry-Flag C zeigt an, ob bei einer Berechnung mit vorzeichenlosen Zahlen ein Über- oder Unterlauf erfolgt ist, d.h. das Ergebnis der Berechnung liegt außerhalb des darstellbaren Bereiches 0...255. Angenommen es müssen zwei 8-Bit-Zahlen addiert werden. Das Ergebnis der Addition umfasst neun Bit und liegt außerhalb des in einem Register darstellbaren Zahlenbereiches 0...255; die Addition ist übergelaufen.
10100011
- 11110011
---------
10110000
Werden dieselben Zahlen subtrahiert, verbleibt an der höchstwertigsten Stelle ein "geborgtes" Bit, welches durch das Carry angezeigt wird.
Zero-Flag Z
Das Zero-Flag Z wird gesetzt, wenn das 8-Bit-Ergebnis der Berechnung null ist.
Negative-Flag N
Das Negative-Flag N wird gesetzt, wenn im Ergebnis das höchstwertige Bit gesetzt ist. Bei vorzeichenbehafteter Arithmetik ist dies als negative Zahl zu interpretieren, sofern nicht durch das V-Flag ein Verlassen des Zahlbereichs angezeigt wird.
Signed- und Overflowflag S und V
Wird mit vorzeichenbehafteten Zahlen gerechnet, so wird das Verlassen des 8-Bit-Zahlenbereiches -128...+127 durch die Flags S und V angezeigt. Der Prozessor selbst unterscheidet nicht zwischen vorzeichenlosen und -behafteten Zahlen. Der Programmierer legt durch Wahl der ausgewerteten Flags (C bei vorzeichenlosen bzw. S/V bei vorzeichenbehafteten) die Interpretation der Zahlen fest.
Half-Carry-Flag H
Das Half-Carry-Flag H zeigt, analog zum Carry-Flag, einen Übertrag zwischen Bit 3 und 4 an. Dies kann in speziellen Anwendungen (z. B. zwei simultane Vier-Bit-Berechnungen mit einem Befehl) nützlich sein.
Übersicht über die arithmetischen Flags
|
[Quelle: www.mikrocontroller.net] Ergebnis des Befehls ADD Rd, Rr Rr| 0 | 1 | 64 | 127 | 128 | 129 | 192 | 255 Rd |( +0)|( +1)|( +64)|(+127)|(-128)|(-127)|( -64)|( -1) ----------+------+------+------+------+------+------+------+------ 0 ( +0)| Z | | | |S N |S N |S N |S N 1 ( +1)| | | | VN |S N |S N |S N | CZ 64 ( +64)| | | VN | VN |S N |S N | CZ | C 127 (+127)| | VN | VN | VN |S N | CZ | C | C 128 (-128)|S N |S N |S N |S N |SV CZ |SV C |SV C |SV C 129 (-127)|S N |S N |S N | CZ |SV C |SV C |SV C |S NC 192 ( -64)|S N |S N | CZ | C |SV C |SV C |S NC |S NC 255 ( -1)|S N | CZ | C | C |SV C |S NC |S NC |S NC Man erkennt: C=1 genau dann wenn die Addition Rd + Rr mit vorzeichenlosen Zahlen überläuft. V=1 genau dann wenn die Addition mit vorzeichenbehafteten Zahlen überläuft. |
Ergebnis des Befehls SUB Rd, Rr bzw. CP Rd, Rr Rr| 0 | 63 | 64 | 127 | 128 | 191 | 192 | 255 Rd |( +0)|( +63)|( +64)|(+127)|(-128)|( -65)|( -64)|( -1) ----------+------+------+------+------+------+------+------+------ 0 ( +0)| Z |S NC |S NC |S NC | VNC | C | C | C 63 ( +63)| | Z |S NC |S NC | VNC | VNC | C | C 64 ( +64)| | | Z |S NC | VNC | VNC | VNC | C 127 (+127)| | | | Z | VNC | VNC | VNC | VNC 128 (-128)|S N |SV |SV |SV | Z |S NC |S NC |S NC 191 ( -65)|S N |S N |SV |SV | | Z |S NC |S NC 192 ( -64)|S N |S N |S N |SV | | | Z |S NC 255 ( -1)|S N |S N |S N |S N | | | | Z Man erkennt: C=1 genau dann wenn die Subtraktion Rd - Rr mit vorzeichenlosen Zahlen unterläuft; äquivalent dazu ist Rd < Rr (vorzeichenlos). S=1 genau dann wenn die Subtraktion mit vorzeichenbehafteten Zahlen unterläuft bzw. Rd > Rr (vorzeichenbehaftet). |
Beispiele für Rechnen mit Assembler
C-Ausdrücke sollen mit ATtiny2313 berechnet werden. Damit der Quelltext leichter lesbar ist wird mittels .def Befehl den Registern symbolische Namen zugewiesen. Nehmen Sie den AVR Befehlssatz zur Hand. Für die Berechnung ist ein 8-Bit-Zahlenraum ausreichend.
| C | a=4; a=a-3; a=a+6; |
a=4; b=5; a=a+b; |
a=4; a=a*2; |
a=4; b=3; a=a+b*3; c=b-a; |
a=4; b=a++; c=--b; |
|---|---|---|---|---|---|
| Assembler | ldi a,4 subi a,3 subi a,-6 |
ldi a,4 ldi b,5 add a,b |
ldi a,4 add a,a |
ldi a,4 ldi b,3 add a,b |
ldi a,4 mov b,a inc a dec b mov c,b |
;Semikolon wird als Kommentareinleitung verwendet
.def a = R16 ;R16 als Variable a verwenden
.def b = R17 ;R17 als Variable b verwenden
.def tmp1 = R18 ;R18 als Hilfs-Variable
; Aufgabe in C-Code:
; a=11;
; a=a-3;
; b=a+5;
; Loesung in Assembler:
ldi a,11 ;lade 11 in a
subi a,3 ;a=a-3
mov b,a ;b=a kopiere a nach b
subi b,-5 ;b=b+5 addi gibts nichtMit Bit-Shift-Befehlen multiplizieren und dividieren
| C | a=2; a=a*2; |
a=-1; a=a*2 |
a=4; a=a/2; |
a=-2; a=a/2; |
a=15; a=-a; |
|---|---|---|---|---|---|
| Binär a= | 0b10 0b100 |
0b11111111 0b11111110 |
0b100 0b10 |
0b11111110 0b11111111 |
0b1111 0b0111 0b0011 0b11111110 |
| Assembler | ldi a,2 lsl a |
ldi a,-1 lsl a |
ldi a,4 asr a |
ldi a,4 asr a |
ldi a,15 asr a asr a neg a |
| Nachdenken | Welchen Wert hat Carry nach LSL? Warum ist ROL nicht geeignet? |
Warum sind LSR und ROR nicht geeignet? | |||
Bei kleineren µC wie dem tiny2313 kann die Alu nicht multiplizieren und dividieren, bei Multiplikationen und Divisionen mit Zweierpotzenzen (2,4,8...) können Bit-Schiebebefehle eine Alternative sein.
Betrachten Sie folgende Befehle in der Formelsammlung und überlegen Sie, ob sie für eine Multipikation oder Division mit 2 geeignet sind: LSL, LSR, ROL, ROR, ASR
andi als Modulo Operator % bei Zweierpotzenzen verwenden
Es gibt keinen % Operator im Befehlssatz. Der Modulo-Operator (%) ermittelt den Rest einer Division. Betrachte folgende Beispiele auf Bit-Ebene und lass Dich erleuchten:
| n | n2 | n % 4 | (n % 4)2 | Berechnung |
|---|---|---|---|---|
| 1 | 0001 | 1 | 0001 | 1 / 4 = 0 Rest 1 |
| 2 | 0010 | 2 | 0010 | 2 / 4 = 0 Rest 2 |
| 5 | 0101 | 1 | 0001 | 5 / 4 = 1 Rest 1 |
| 10 | 1010 | 2 | 0010 | 10 / 4 = 2 Rest 2 |
Mit welchem logischen Befehl lässt sich genau so eine Berechnung erreichen?
Erstellen Sie ein Programm zur Berechnung des Problem-Ausdrucks und testen Sie Ihre Lösung mit sinnvollen Werten!
Ermitteln Sie die Ausführungszeit Ihres Berechnungs-Programms in Taktzyklen.
Übung und Training
Erstellen Sie Assemblercode zur Berechnung der Ausdrücke und testen Sie Ihre Lösung mit sinnvollen Werten:
| C | b = (a + 2) / 4 | b = a % 2 | b = a * 3 | b = (a - 3) * 2 + (a % 4) | y = -4x+5*4 |
|---|---|---|---|---|---|
| Assembler | Lösungmov b,a subi b,-2 asr b asr b |
Lösungmov b,a andi b,1 |
Lösungmov b,a add b,a add b,a |
Lösungmov b,a subi b,3 lsl b mov tmp,a andi tmp,3 add b,tmp |
Lösungmov y,x neg y lsl y lsl y subi y,-20 |
Rechnen in Assembler
Geben Sie den Inhalt von SREG-Flags N,Z,C und dem Register R16 nach der Ausführung des Befehls an. Gehen Sie davon aus, dass vor dem ersten Befehl N,Z,C gelöscht (0) sind. Hinweis: Der com-Befehl setzt immer das C-Flag
| Befehl | SREG | R16 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Z | C | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| ldi R16, 8 | |||||||||||
| com R16 | |||||||||||
| subi R16, 5 | |||||||||||
| clr R16 | |||||||||||
| neg R16 | |||||||||||
| Befehl | SREG | R16 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Z | C | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | |
| ldi R16, 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| com R16 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| subi R16, 5 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| clr R16 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| neg R16 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
