MezData-Logo

For-Schleife Häuserproblem

Problem:

Ein Programm soll die Anzahl der Leitungen ermitteln, die nötig sind um n Häuser mit jeweils einer Leitung direkt miteinander zu verbinden.

Problem-Analyse:

Graphik Problemgröße Lösung
n = 1 0 Leitungen
n = 2 1 Leitung
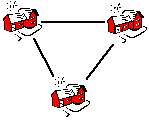n = 3 3 Leitungen
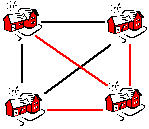n = 4 Wenn das 4. Haus ins Spiel kommt, muss es mit den restlichen drei Häusern verbunden werden.
Hierzu werden drei weitere Leitungen benötigt:

Bisher 3 plus 3 = 6 Leitungen
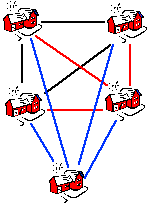n = 5 Beim 5. Haus braucht man schon 0+1+2+3+4 = 10 Leitungen.

D.h. das n-te Haus wird mit n-1 Leitungen an die vorhandenen Häuser angeschlossen.

(0+1+2+3)+4 = 10
  n Um das Problem für beliebige n lösen zu können brauchen wir ein Programm das die Summe

0+1+2+..+n-1 ausrechnet, die Summe der Zahlen von 0 bis n-1.

Wie würde man so eine Summe von "Hand" ausrechnen?

0+1=1; 1+2=3; 3+3=6; 6+4=10 usw. bis summe + n-1 = Leitungen. Man bräuchte etwas, das die Zahlen von 0 bis n-1 hochzählt:

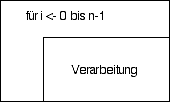For-Schleife (i hochzählen)

for (i = 0; i < n; i = i+1)
  Verarbeitung
i = 0 ist die Initialisierung der Zählvariablen i.

i < n ist die Schleifen-Invariante, solange diese Bedingung gilt, wird weitergezählt.

i = i+1 ist die Schrittweite, sie gibt an, wie die Zählvariable bei jedem Schleifendurchlauf erhöht wird.

Fehlt nur noch die Verarbeitung in der Schleife, die Zahlen aufsummieren:

summe = summe + i; // bei jedem Durchlauf ist i um eins erhöht und wird zum bisherigen Ergebnis addiert

C++: Die ganze Lösung

Struktogramm

lokale Variablen n,summe,i :Integer

Quelltext

int n,summe,i;

cout << "Wieviele Haueser sollen verbunden werden ? ";
cin >> n; // Eingabe n

summe = 0; // summe initialisieren
for (i=0;i<n;i=i+1){ // fuer i <- 0 bis n-1

  summe = summe + i;
} // -fuer i <- 0 bis n-1
cout << "\nEs werden " << summe << " Leitungen gebraucht\n";

Java: Die ganze Lösung

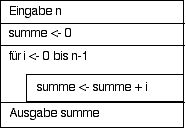
Struktogramm

lokale Variablen n,summe,i :Integer

Quelltext

int n,summe,i;

Eingabe n; // Hier entsprechende Java-Methoden verwenden
summe = 0; // summe initialisieren

for (i=0;i<n;i=i+1){ // fuer i <- 0 bis n-1
  summe = summe + i;
} // -fuer i <- 0 bis n-1
Ausgabe summe; // Hier entsprechende Java-Methoden verwenden

Job: Implementieren und testen Sie die Lösung!

Typische For-Schleife

for (zaehlvar = startwert;zaehlvar <= endwert;zaehlvar++)
  Verarbeitung
Hinweis: zaehlvar++ ist die Abkürzung für zaehlvar = zaehlvar + 1
Wenn man eine einfache Schleife braucht die von einem Startwert zu einem Endwert zählt bietet sich die For-Schleife an.

Ist die Schrittweite der Zählvariablen eins, braucht sie im Struktogramm nicht unbedingt angegeben werden.

Verarbeitung

Es gibt drei Möglichkeiten für Verarbeitung innerhalb der For-Schleife:

Beispiel leere Anweisung eine Anweisung Block von Anweisungen 
for(...)
  Verarbeitung
 
for(...);
 
for (...)
  Anweisung;
 
for(...){
  Anweisung 1
  Anweisung 2
  ...
  Anweisung n
}

Allgemeine For-Schleife

for (Initialisierung;Bedingung;Schrittweite)
  Verarbeitung // Rumpf der Schleife

Reihenfolge der Bearbeitung

Beim Eintritt in die Schleife wird die Initialisierung ausgeführt.

Dann wird die Bedingung ausgewertet, ist sie erfüllt, wird der Rumpf der Schleife verarbeitet.

Nach Verarbeitung des Rumpfes kommt die Schrittweite im Schleifen-Kopf, z.B. das Inkrement.

Nun wird wieder die Bedingung überprüft, ist sie immer noch erfüllt, geht es wieder in den Rumpf.

Der Kreislauf dauert solange bis die Bedingung nicht mehr erfüllt ist, die Schleife wird verlassen.

Bedingung

Die Bedingung gibt vor wie lange die Schleife ausgeführt wird.

Schrittweite

Dieser Abschnitt wird nach der Verarbeitung des Schleifen-Rumpfes ausgeführt. Eine Erhöhung einer Zählvariablen nennt man Inkrement z.B. i++ oder i = i +2

Eine Erniedrigung einer Zählvariablen nennt man Dekrement z.B. i-- oder i = i -10

Initialisierung

Es besteht die Möglichkeit im Initialisierungs-Abschnitt Variablen auch zu Definieren, diese Variablen gelten dann nur innerhalb der For-Schleife:

ohne Definition mit Definition 
int i=1,summe=1;
for (i=0,summe=0;i<4;i++)
  summe = summe + i;
Ausgabe i;
Ausgabe summe;
 
int i=1,summe=1;
for (int i=0,summe=0;i<4;i++)
  summe = summe + i;
Ausgabe i;
Ausgabe summe;
i: 4

summe: 6

 i: 1

summe: 1
Werden Variablen innerhalb eine For-Schleife definiert überdecken sie gleichnamige Variablen aus der Umgebung der Schleife, sie sind lokal innerhalb der Schleife.

Nach dem Schleifenende sind diese lokalen Variablen verschwunden, die überdeckten Variablen kommen wieder zum Vorschein.

InformationEinfache Lösung des Problems ohne Schleife

Früher hat man Schüler zum Üben der Addition die Aufgabe gegeben, die Summe der Zahlen bis 100 zu bilden. Eine mords Arbeit...

Da gab es einen Schüler namens Gauß, dem das zu langweilig war, er hat sich Gedanken gemacht, wie man diese Summen schneller bilden kann.
n sei ungerade (Beispiel 5) n sei gerade (Beispiel 6)
Fasse Summanden nach obigem Prinzip zusammen:

Jede Paarung ergibt n (hier 5). Wieviele Paare können gebildet werden?

(n+1)/2 (hier 3) da es bei ungeraden n mit der 0 n+1 Zahlen sind

Lösung: Anzahl der Paare * Wert der Paarung = (n+1)/2 * n

 Fasse Summanden nach obigem Prinzip zusammen:

Jede Paarung ergibt n+1 (hier 7). Wieviele Paare können gebildet werden?

n/2 (hier 3)

Lösung: Anzahl der Paare * Wert der Paarung = n/2 * (n+1)
Mit etwas Umformen erkennt man leicht, das die Lösung für beide Fälle identisch ist!
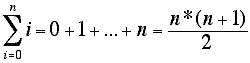Summe von i = 0 bis n über i

Fragen

Wozu braucht man For-Schleifen?

Was versteht man unter Initialisierung bei einer For-Schleife?

Wo befindet sich der Schrittweiten-Abschnitt einer For-Schleife, wann wird er ausgeführt?

Wie sieht eine typische For-Schleife aus, erklären Sie den Aufbau und die Wirkungsweise anhand eines Beispiels (Struktogramm und Quelltext).

In welchem Fall kann man im Struktogramm einer For-Schleife das Inkrement weglassen?

Welche Auswirkungen haben Definition von Variablen im Initialisierungs-Abschnitt einer For-Schleife?