Lottozahlen
Eine Liste für 6 Lottozahlen ist zunächst mit 0en gefüllt:
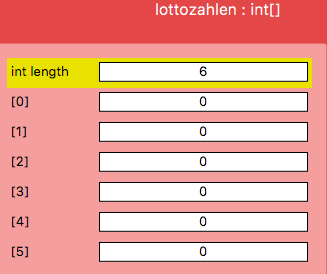
Der Zufallsgenerator kennt nicht die bereits gezogenen Kugeln.
Daher schauen, ob die Zufallszahl schon gezogen wurde...
Ergänzen Sie den Quellcode für eine Lottoziehung.
Lösung anzeigen..public class LottoAufgabe{ static int lottozahlen[]= new int[6]; static void ausgeben(){ int i; for(i=0; i<6;i++){ System.out.print(lottozahlen[i]+" "); } System.out.println(); } static int zufall(){ return (int) (Math.random()*50)+1; // 1..49 } static void ziehung(){ int kugel=0; // Anzahl gezogener Kugeln int zahl,i; boolean vorhanden; while (kugel<6){ // solange noch nicht alle Kugeln gezogen zahl = zufall(); vorhanden = false; for(i=0;i<kugel;i++){ // alle gezogenen Kugeln // Aufgabe } if(!vorhanden){ // war die Kugel nicht vorhanden? // Aufgabe } } } }
Merker Klasse (Einfügen in Liste)
In einer Klasse Merker sollen mehrere ganze Zahlen gespeichert werden können. Zunächst sind 3 Speicher angelegt.

| Merker |
|---|
| speicher[] : GZ eFindex: GZ |
anhaengen(n:GZ) vorneEinfuegen(n:GZ) |
Um speichern, welcher Platz schon belegt ist wird ein Attribut eFindex für den ersten freien Index-Platz in der Liste verwendet. anhaengen(..) speichert am Ende. Wenn alle Plätze belegt sind ist die Liste voll.
Einfügen am Anfang
Beim Einfügen am Anfang muss zuerst der bisherige Inhalt nach hinten verschoben werden um Platz für das nächste Element zu schaffen.
Ergänzen Sie den Quellcode für vorneMerken(n:GZ).
Lösung anzeigen..Nur Neues merken
Eine Operation merke(n:GZ) schaut zuerst nach, ob der Wert schon gemerkt wurde und fügt nur neue Werte am Ende ein. Entwickeln Sie eine Lösung.
Lösung anzeigen..public class MerkerAufgabe{ static int[] speicher = new int[3]; // Speicherliste static int eFindex; // = 0; // erster freier Index static void anhaengen(int n){ if (eFindex < speicher.length) speicher[eFindex++]=n; else System.out.println("Die Liste ist voll: "+eFindex); } static void vorneEinfuegen(int n){ int i; if (eFindex < speicher.length){ // Aufgabe speicher[0]=n; eFindex++; } else System.out.println("Die Liste ist voll: "+eFindex); } }
Erweitern des Speichers

Der Zahlenspeicher soll verdoppelt werden, bei einfachen Int-Listen ist eine nachträgliche Erweiterung der Speicherkapazität nicht vorgesehen.
Daher wird zunächst eine neue grössere Liste erzeugt und dann der Inhalt der alten Liste hineinkopiert. Schließlich wird der zahl-Verweis auf die neue Liste gesetzt.
Für das Kopieren müssen schlicht die Indizies der beiden Listen durchgezählt werden:
für i von 0 bis zahl.length-1 kopiere neu[i] <- speicher[i]
Genau dafür ist die For-Schleife gedacht:

void verdoppleSpeicher(){
int[] neu = new int[speicher.length*2]; // neue Liste erzeugen
int i;
for (i=0;i<speicher.length;i++) // in neue Liste kopieren
neu[i]=speicher[i];
speicher=neu; // Verweis nun auf neue Liste
}Implementieren und Testen Sie die Methode verdoppleSpeicher().
Erstellen Sie ein Struktogramm. Lösung

Erweitern Sie die Methode merke() mit der Speicherverdopplung.
Lösung anzeigen..
Sortieren mit Bubble-Sort

Einfachster Sortieralgorithmus: Bubblesort
Von unten nach oben durch die Liste gehen und zwei benachbarte Elemente vergleichen, falls das untere kleiner (leichter) ist tauschen. Die leichteren Elemente blubbern hoch wie Blasen.
Erstellen Sie aus dem Struktogramm die Operation bubbleSort() in der Merker-Klasse.
Testen Sie mit diesen Daten vor und nach dem Sortieren.
static void test(){
merke(23);
merke(12);
merke(20);
merke(3);
merke(1);
}Warum wird in bubbleSort() nach jedem Durchlauf das i erhöht?
Nach einem Wert suchen
Bei einer ungeordneten Liste müssen alle Werte betrachtet werden um entscheiden zu können ob ein Wert nicht vorhanden ist. Geordnete, sortierte Listen bringen einen Effizienzgewinn beim Suchen.
Entwickeln Sie eine Operation suche(n:GZ):Boolean, die in einer sortierten Liste entscheidet ob n vorhanden ist.
Lösung anzeigen..Sortierte Listen sind besser
Einfügen nach binärer Suche einer passenden Stelle ist effizient:
Lösung anzeigen..