Lösung eines Problems durch Rekursion
Eine Operation kabel(n:GZ):GZ soll die Anzahl der Kabel ermitteln, die nötig sind um n Häuser mit jeweils einem Kabel direkt miteinander zu verbinden. Bei vielen Aufgabenstellungen ist eine Lösung leichter zu finden, indem sie rekursiv definiert wird. Beispiel:
| Graphik | Anzahl der Häuser | Ergebnis | Funktion |
|---|---|---|---|
| n = 1 | 0 Kabel | kabel(1)->0 | |
| n = 2 | 1 Kabel | kabel(2)->1 | |
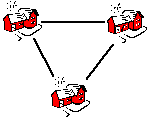 |
n = 3 | Das 3. Haus wird mit den ersten beiden Häusern verbunden: 1 + 2 = 3 Kabel |
kabel(3)=kabel(2)+2->3 |
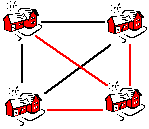 |
n = 4 | Beim 4. Haus braucht es 3 weitere Kabel: 3 + 3 = 6 Kabel |
kabel(4)=kabel(3)+3->6 |
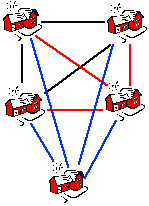 |
n = 5 | Beim 5. Haus: 6 + 4 = 10 Kabel (0+1+2+3)+4 = 10 |
kabel(5)=kabel(4)+4->10 |
| n | Bei n Häusern:
0+1+2+..+n-1 die Summe der Zahlen von 0 bis n-1. |
kabel(n)=kabel(n-1)+n-1 |
public class Kabel{ static int kabel(int n){ if (n<=1) return 0; return kabel(n-1)+n-1; } }
Bei vielen Problemen ist leicht zu erkennen, was bei einer Vergrösserung von n nach n+1 dazu kommt, bzw. das Problem der Grösse n lässt sich mit dem Ergebnis von n-1 einfach berechnen.
Eine rekursive Lösung ist schnell geschrieben.
Beim Aufruf von kabel(4) könnte dieser Ablauf angenommen werden:
kabel(4)=>(kabel(3)+3)=>((kabel(2)+2)+3)=>(((kabel(1)+1)+2)+3)=>(((0)+1)+2)+3)=>((1+2)+3)=>(3+3)=>6
Auf dem Weg bis ein Ergebis von kabel(1) fest steht wird kabel() als Unterprogamm immer wieder aufgerufen und erst auf dem Rückweg werden die Unterprogrammaufrufe wieder geschlossen. Es würde bis zum Ergebnis von kabel(1) der Bedarf an Speicher ansteigen.
Auflösen einer Rekursion durch Iteration
Viele rekursiv gelöste Probleme lassen sich durch eine Schleife (Iteration) bewältigen, die weniger speicherintensiv ist. Entwickler versuchten vor optimierenden Compilern daher Rekursion möglichst zu vermeiden. Mittlerweile erkennen Compiler auflösbare Rekursionen (Endrekursionen) und ersetzen sie durch Iterationen. Bei dem Kabel-Problem ist eine Lösung mit for-Schleife greifbar nahe:
Erstellen Sie eine Operation kabelFor(n:GZ):GZ. Lösung anzeigen..
Aufgabe: Klingende Gläser
Auf einer Fete sind bereits 17 Leute. Sebastian kommt als 18. Jeder Neuankömmling stößt mit jedem an. Sebastian wird gefragt wie oft nun nach seiner Ankunft die Gläser schon geklungen haben. "Die Frage kann ich leicht beantworten, wenn derjenige, der vor mir gekommen ist, sein Ergebnis nennt." sagt Sebastian. Alle lachen, Timo sagt: "Ursula kam vor dir und hat auch schon so gefragt!" "Timo hat gut lachen", sagt Sabine, "er hat niemand zu fragen brauchen, er war nämlich der erste heute Abend und brauchte bloß einmal mit dem Gastgeber anzustoßen."
| Personen | 0 | 1 | 2 | 3 | 4 | n |
|---|---|---|---|---|---|---|
| Anstöße | 0 | 0 | 1 |
Analysieren Sie das Problem (Tabelle)
Entwickeln Sie eine Operation Summe.angestossen(n:GZ):GZ und ein Struktogramm für die Lösung. Lösung anzeigen..
Permutation (Fakultät, Produkt über n)
Man stelle sich folgendes Problem vor, wie viele Möglichkeiten gibt es 2 Hüte auf 2 Haken zu verteilen? Wieviele Möglichkeiten gibt es bei 3 Hüten und 3 Haken usw. Man nennt diese Problemklasse auch Permutation.
| Möglichkeit Nr. | Haken 1 | Haken 2 |
|---|---|---|
| 1 | Hut 1 | Hut 2 |
| 2 | Hut 2 | Hut 1 |
Wenn bei drei Hüten einer auf dem ersten Haken hängt, bleiben für die restlichen beiden Hüte nur noch zwei Möglichkeiten. Jeder der drei will mal der erste sein, somit 3*2 Möglichkeiten.
| Nr. | Haken 1 | Haken 2 | Haken 3 |
|---|---|---|---|
| 1 | Hut 1 | Hut 2 | Hut 3 |
| 2 | Hut 1 | Hut 3 | Hut 2 |
| 3 | Hut 2 | Hut 1 | Hut 3 |
| 4 | Hut 2 | Hut 3 | Hut 1 |
| 5 | Hut 3 | Hut 1 | Hut 2 |
| 6 | Hut 3 | Hut 2 | Hut 1 |
Rekursive Definition der Möglichkeiten: m(1)=1; sonst m(n)=m(n-1)*n
Entwickeln Sie eine rekursive Operation Hut.m(n:GZ):GZ
Lösung anzeigen..
Mathe-Einschub
In der Mathematik wird das '!' Zeichen für die Fakultätsfunktion benutzt:
| 1! = 1 | 2! = 2 | 3! = 6 | Allgemein: x!= 1*2*...*x |
|---|
D.h.. Sollen 4 Hüte auf 4 Haken verteilt werden, gibt es 4! =1*2*3*4 = 24 Möglichkeiten!
Entwickeln Sie eine iterative Operation Fakultaet.fak(n:GZ):GZ, die das Produkt von 1..n berechnet. Lösung anzeigen..
Fibonacci
In Lehrbuch der Mathematik aus dem Mittelalter stellte "Leonard der des Bonaccus" (filius bonacci = fibonacci) die folgende Aufgabe:
Wieviele Kaninchenpaare werden im Laufe eines Jahres, von einem Paar ausgehend geboren?
Dabei wirft jedes Paar monatlich ein weiteres Paar, das wiederum nach Ablauf des 2.Lebensmonats ein weiteres Paar wirft. Die Populationsfolge wird auch Fibonacci-Folge genannt.
Erstellen Sie eine Operation Fibonacci.fib(n:GZ):GZ, die die existierenden Kaninchenpaare im Montat n zurückgibt.
Tipp: 1, 1, 2, 3, 5, 8, 13, ... fib(n) = fib(n-1) + fib(n-2)
Erstellen Sie eine Operation Fibonacci.tabelle(n:GZ), die eine formatierte Tabelle der Population bis zum Monat n ausgibt. Lösung anzeigen..
Beachten Sie die Dauer der Rechenzeit ab n=40 und wieso wird das Ergebnis ab n=46 negativ?
