:TI-BASIS: Datendarstellung in Digitalen Systemen

Elementare Datentypen für logische Werte und Zahlen

US-Darstellung der Kommata (mit Punkt) und Tausender-Trennzeichen (mit Komma) z.B. 1,000.0 für eintausendkommanull.
C++ Typen für 32-Bit Betriebssystem, genaue Umsetzung ist Compiler und vom Betriebssystem abhängig!
Delphi Typen für 32-Bit Betriebssystem, genaue Umsetzung ist Compiler und vom Betriebssystem abhängig!

Datentyp	Beschreibung	Bits	Wertebereich	Java-Typ	C++-Typ	Delphi / Pascal-Typ
Void	leer / ohne Referenz	?	-	void / null	void	- / NIL
Boolean	Log. Wert	8	true, false	boolean	bool	BOOLEAN
Char	Zeichen	8	0..255	-	unsigned char	CHAR
Char	Zeichen	16	\u0000..\uFFFF; Unicode	char	-	-
Byte	ganze Zahl	8	-128..127	byte	signed char; char	SHORTINT
Byte	pos. ganze Zahl	8	0..255	-	unsigned char	BYTE
Short	ganze Zahl	16	-32,768..32,767	short	short int, short	SMALLINT
Short	pos. ganze Zahl	16	0..65535	-	unsigned short	WORD
Integer	ganze Zahl	32	-2,147,483,648..2,147,483,647	int	int, long	INTEGER, LONGINT
Integer	pos.ganze Zahl	32	0..4,294,967,295	-	unsigned int	CARDINAL
Long	ganze Zahl	64	-2⁶³..2⁶³-1	long	-	-
Float	IEEE 754 Gleitkommazahl einfache Genauigkeit	32	ca. +-1.4 * 10^-45 .. +-3.4 * 10³⁸ Genauigkeit ca. 7 Stellen	float	float	SINGLE
REAL	Gleitkommazahl Delphi / Pascal Ist ineffizient!	48	ca. +-2.9 * 10^-39 .. +-1.7 * 10³⁸ Genauigkeit ca. 11 Stellen	-	-	REAL
Double	IEEE 754 Gleitkommazahl doppelte Genauigkeit	64	ca. +-4.9 * 10^-324 .. +-1.8 * 10³⁰⁸ Genauigkeit ca. 15 Stellen	double	double	DOUBLE
Long Double	Gleitkommazahl	80	ca. +-3.4 * 10^-4932 .. +-1.1 * 10⁴⁹³² Genauigkeit ca. 19 Stellen	-	long double	EXTENDED

Logische Werte (Boolean, boolean, bool)

Logische Werte sind die Wahrheitswerte Falsch und Wahr (engl.:false bzw. true).
Sie werden meist durch die Buchstaben F und T oder L und H abgekürzt, haben den binären Wert 0 und 1(ungleich 0).

Ganzzahlige Zahlen (byte, short, long, int)

Vorzeichenlose Zahlen (unsigned char, unsigned short, unsigned int)

Zahlen werden im Rechner Im Dualsystem dargestellt. Dabei ergibt die Anzahl der Bits die Grösse der größten darstellbaren Zahl, den darstellbaren Zahlenbereich, zunächst für die vorzeichenlosen Zahlen (natürlichen Zahlen):

Darstellung positiver Zahlen (natürlicher Zahlen)
Bits	1	2	3	4	8	16	32	n
Bezeichnung	Bit	-	-	Nibble	Byte	Word	DWord	Allgemein
Anzahl der Zahlen	2	4	8	16	256	65.536	4.294.967.296	2ⁿ
pos. Zahlenbereich	0..1	0..3	0..7	0..15	0..255	0..65.535	0..4.294.967.295	0..2ⁿ-1
Info: Darstellung in verschiedenen Zahlensystemen
Grösste Zahl in Dual	1₂	11₂	111₂	1111₂	1111 1111₂	1111 1111 1111 1111₂	32 Einsen
Grösste Zahl in Oktal	1₈	3₈	7₈	17₈	377₈	177777₈
Grösste Zahl in Hex	1₁₆	3₁₆	7₁₆	F₁₆	FF₁₆	FFFF₁₆	FFFF FFFF₁₆

Info: Die vorzeichenlosen Zahlen kann man mit den natürlichen Zahlen assoziieren, aber Achtung: Digitale Systeme haben immer nur endlich viel Speicherplatz, es gibt jedoch unendlich viele natürliche Zahlen! Folglich kann immer nur eine (sehr kleine) Teilmenge von IN dargestellt werden.

Negative Zahlen

Problem: Wie können negative Zahlen in digitalen Systemen dargestellt werden?
Lösung: Man verwendet das vorderste Bit als Vorzeichen, Beispiel mit 4 Bit:

0 = 0000	4 = 0100
1 = 0001	5 = 0101
2 = 0010	6 = 0110
3 = 0011	7 = 0111

-0 = 1000	-4 = 1100
-1 = 1001	-5 = 1101
-2 = 1010	-6 = 1110
-3 = 1011	-7 = 1111

Ist das vorderste Bit 0 ist die Zahl positiv sonst negativ. Diese Darstellung nennt man Vorzeichendarstellung.

Die Vorzeichendarstellung hat aber eine Reihe von Nachteilen:

Die Null wird durch zwei Bitfolgen dargestellt: 0000 und 1000
Das Rechnen ist so nicht so einfach

Zweierkomplement-Darstellung

Prinzip für 4 Bit: Zähle von 0 aufwärts bis zu +7, dann gehts bei -8 bis zur -1 weiter.

0 = 0000	4 = 0100
1 = 0001	5 = 0101
2 = 0010	6 = 0110
3 = 0011	7 = 0111

-8 = 1000	-4 = 1100
-7 = 1001	-3 = 1101
-6 = 1010	-2 = 1110
-5 = 1011	-1 = 1111

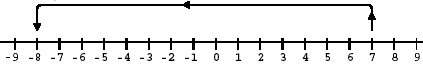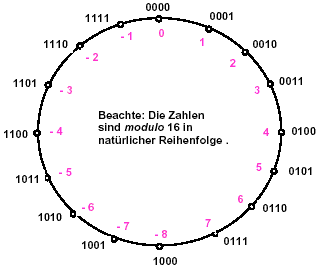Wenn das vorderste Bit = 1, ist die Zahl negativ!

Aufgabe: Berechne in der Zweierkomplementdarstellung 5 + (-3)
Lösung: 5 = 0101; -3 = 1101; 0101+1101 = 10010 =Übertrag weg wegen modulo 16=> 0010 = 2

Wie kann das Zweierkomplement zu einer gegebenen Zahl berechnet werden?

Zahl in Dual umwandeln, bitweise invertieren, dann 1 addieren. Beispiel:
Gesucht -6: 6₁₀ = 0110 =invertieren=> 1001 + 1 = 1010₂
Gesucht -1; 1₁₀ = 0001 =invertieren=> 1110 +1 = 1111₂

Rückumwandeln einer negativen Zahl funktioniert genauso:
Gesucht: 1101₂ =invertieren=> 0010 + 1 = 0011 = 3₁₀

Gebrochene Zahlen

Problem: Wie kann die Zahl 0,5 als Dualzahl dargestellt werden?
Lösung: 0,5₁₀ = 0,1₂ Nach dem Komma stehen im Dualsystem die Brüche 2^-mmit m Stelle nach dem Komma.

Stelle	n	..	2	1	0	-1	-2	..	-m
Wertigkeit	2ⁿ	..	2²	2¹	2⁰	2^-1	2^-2	..	2^-m
Wert	-	..	4	2	1	0,5	0,25	..	-
Beispiel			0	1	0	1	1
2,75 =			0*4 +	1*2 +	0*1 +	0,5 +	0,25

Im Speicher n+m Bits
n Bits vor dem Komma	m Bits nach dem Komma

Darstellung gebrochener Zahlen

Aufgabe: Gegeben seien 8 Bit für die Darstellung einer gebrochenen Zahl, n=4;m=4. Wie genau kann 1/3 dargestellt werden?
Lösung:

Gleitkomma-Zahlen (REAL, Float, Double, long double)

Problem: Wie können bei gegebenem Speicherplatz möglichst viele Reale Zahlen (Gleitkomma-Zahlen) möglichst genau dargestellt werden?

Bsp: 1 200 001 würde doch als 1.2 Mio noch genau genug sein: 1.2 * 10⁶ . Wissenschaftlich 1.2 E6 im Taschenrechner dargestellt.

Genau das ist der Trick, man verwendet beim Kodieren einen Teil der Bits für den Exponenten, hier die 6 und den anderen Teil für die Mantisse, die 1.2.

Komponenten einer Gleitkomma-Zahl

Das Vorzeichenbit: V, gibt an, ob die Zahl positiv oder negativ ist
Dem Exponenten: E, ist eine Vorzeichen-Dualzahl (oder von einer vorzeichenlosen Zahl wird ein bestimmter Betrag (bias) abgezogen) mit der die Mantisse zu multiplizieren ist
Der Mantisse: M = 1.m₁m₂m₃m₄..m_n, einer normierten Dualzahl, bei der die höchstwertigste Stelle geklaut werden kann

Die Zahl ergibt sich aus: (-1) *V * (1+m₁*2^-1+m₂*2^-2+..+m_n*2^-n)*2^E

Spezielle Kodierungen bei gegebener Bit-Anzahl nach IEEE 754

32 Bit (einfache Genauigkeit)

Short Real, Float	Bit Nummer	31	30..23	22..0
ca. +-1.4 * 10^-45 .. +-3.4 * 10³⁸ Genauigkeit ca. 7 Stellen	Anzahl Bits	1	8	23
	Bedeutung	V	Exponent	Mantisse

64 Bit (doppelte Genauigkeit)

Long Real, Double	Bit Nummer	63	62..52	51..0
ca. +-4.9 * 10^-324 .. +-1.8 * 10³⁰⁸ Genauigkeit ca. 15 Stellen	Anzahl Bits	1	11	52
	Bedeutung	V	Exponent	Mantisse

C++ & Delphi: 80 Bit (erweiterte Genauigkeit)

long double, EXTENDED	Bit Nummer	79	78..64	63	62..0
ca. +-3,4 * 10^-4932 .. +-1,1 * 10⁴⁹³² Genauigkeit ca. 19 Stellen	Anzahl Bits	1	15	1	63
	Bedeutung	V	Exponent	i??	Mantisse

Normieren von Zahlen

Ziel der Normierung ist folgendes Aussehen der Dualzahlen: 1.m₁m₂m₃m₄..m_n, dabei wird das Komma verschoben, das klappt bei allen Zahlen ungleich null, Beispiel:

11₁₀ = 1011₂ = 1011₂ * 2⁰ = 101.1₂ * 2¹ = .. = 10.11₂ * 2² = 1.011₂ * 2³ = (1+1/4 + 1/8)*8 = 8+2+1 = 11

Da nun vorne immer eine 1 steht kann man die auch weglassen!

Zeichen (char)

American Standard Code for Information Interchange

ASCII-Tabelle (7-Bit)

Dez	Hex	Zeichen	Dez	Hex	Zeichen	Dez	Hex	Zeichen	Dez	Hex	Zeichen	Dez	Hex	Zeichen
0	00	Nul	26	1A	SUB	52	34	4	78	4E	N	104	68	h
1	01	SOH	27	1B	ESC (Escape)	53	35	5	79	4F	O	105	69	i
2	02	STX	28	1C	FS	54	36	6	80	50	P	106	6A	j
3	03	ETX	29	1D	GS	55	37	7	81	51	Q	107	6B	k
4	04	EOT (End Of Transmission)	30	1E	RS	56	38	8	82	52	R	108	6C	l
5	05	ENQ	31	1F	US	57	39	9	83	53	S	109	6D	m
6	06	ACK	32	20	SP (Space)	58	3A	:	84	54	T	110	6E	n
7	07	BELL (Klingel)	33	21	!	59	3B	;	85	55	U	111	6F	o
8	08	BS (Back Space)	34	22	"	60	3C	<	86	56	V	112	70	p
9	09	Hor. Tabulator	35	23	#	61	3D	=	87	57	W	113	71	q
10	0A	LF (Line Feet)	36	24	$	62	3E	>	88	58	X	114	72	r
11	0B	Ver. Tabulator	37	25	%	63	3F	?	89	59	Y	115	73	s
12	0C	FF (Form Feet)	38	26	&	64	40	@	90	5A	Z	116	74	t
13	0D	CR (Carriage Return)	39	27	'	65	41	A	91	5B	[	117	75	u
14	0E	SO	40	28	(	66	42	B	92	5C	\	118	76	v
15	0F	SI	41	29	)	67	43	C	93	5D	]	119	77	w
16	10	DLE	42	2A	*	68	44	D	94	5E	^	120	78	x
17	11	DC1	43	2B	+	69	45	E	95	5F	_	121	79	y
18	12	DC2	44	2C	,	70	46	F	96	60	'	122	7A	z
19	13	DC3	45	2D	-	71	47	G	97	61	a	123	7B	{
20	14	DC4	46	2E	.	72	48	H	98	62	b	124	7C	\|
21	15	NAK	47	2F	/	73	49	I	99	63	c	125	7D	}
22	16	SYN	48	30	0	74	4A	J	100	64	d	126	7E	~
23	17	ETB	49	31	1	75	4B	K	101	65	e	127	7F	DEL (Delete)
24	18	CAN	50	32	2	76	4C	L	102	66	f
25	19	EM	51	33	3	77	4D	M	103	67	g

Unicode & Co.

Es gibt zwei weitere häufig genannte Zeichencodes, die praktisch zeichengleich sind:

UCS: [ISO10646]: "Information Technology -- Universal Multiple-Octet Coded Character Set (UCS) -- Part 1: Architecture and Basic Multilingual Plane", ISO/IEC 10646-1:1993. The current specification also takes into consideration the first five amendments to ISO/IEC 10646-1:1993.
Unicode: Link: http://www.unicode.org/

Wesentliche Punkte:

Die ersten 128 Zeichen dieser Codes sind ASCII-kompatibel, die ersten 256 Zeichen sind kompatibel zu dem hierzulande häufig verwendeten Code ISO-8859-1 genannt Latin-1.
ASCII und Latin-1 sind die klassischen 8-Bit-Codes.
UCS und Unicode sind die neueren 16-Bit-Codes - und enthalten alle gängigen Zeichen dieser Welt.
Herkömmliche Programmiersprachen lassen meist keine Zeichen aus ASCII-Erweiterungen zu. Java erlaubt als erste der weit verbreiteten Sprachen die Verwendung beliebiger Unicode-Zeichen. Allerdings heißt dies noch lange nicht, daß jede Java-Implementierung einen Editor zur Eingabe von Unicode mitliefern würde.

Escape-Sequenzen für Unicode

Zeichen- kombination	Bedeutung / übernommenes Zeichen	Zeichen- kombination	Bedeutung / übernommenes Zeichen
\a	alert (akustisches oder sichtbares Signal)	\\	\ (invertierter Schrägstrich, backslash)
\b	backspace (ein Zeichen zurück)	\'	' (Hochkomma, quote)
\n	new line (Neue Zeile)	\"	" (Anführungszeichen)
\r	carriage return (Wagenrücklauf)	\?	? (Fragezeichen)
\t	horizontal tabulator	\ddd	Übernahme des durch die Oktalziffern ddd festgelegten Zeichens
\v	vertical tabulator	\xhh	Übernahme des durch die Hex-Ziffern hh festgelegten Zeichens
\f	form feed (vorrücken bis zur nächsten Seite)	\udddd	Unicode-Zeichen in Hexadezimalschreibweise z.B. \u0020 für Leerzeichen

Zeichenketten (String, string, char[])

Fortlaufender Text besteht aus einer Folge von einzelnen Zeichen, einer Zeichenkette (engl.: String). Die Codes der einzelnen Zeichen werden aneinander gefügt.
Beispiel: Der Text "Hallo Welt" wird so dargestellt:

Zeichenfolge	'H'	'a'	'l'	'l'	'o'	' '	'W'	'e'	'l'	't'
Dez. Nummer in ASCII	072	097	108	108	111	032	087	101	108	116
Hex in ASCII	48	61	6C	6C	6F	20	57	65	6C	74
Bitfolge im Rechner	01001000	01100001	01101100	01101100	01101111	00100000	01010111	01100101	01101100	01110100

Strings

Java	Klassisch: C	Moderner: C++	Kompatibel: mit Delphi / Pascal
String-Klasse	char-Array	string-Klasse	AnsiString-Klasse entspricht String-Datentyp aus Delphi	SmallString<n> entspricht String[n] aus Delphi
String s = "Hugo"	char s[] = "Hugo"	string s = "Hugo"	String s = "Hugo"	SmallString<40> s = "Hugo"
Strings beginnen mit dem Index 0			Strings beginnen mit dem Index 1 wie bei Pascal üblich

Hinweis: Bei Java gibt es noch StringBuffer-Klasse