:TI-BASIS: Funktionen / Funktionstabellen

Die Schaltalgebra ist die Lehre von der Verknüpfung mehrerer Eingangsvariablen (X0, X1,..Xn) mit oft nur einer Ausgangsvariablen (Y).

Y = f(Xn..,X1,X0) alternativ: Q=f(D,C,B,A)

Dabei nehmen alle Variablen nur zwei Zustände (0 oder 1) an (Binäres Signal).

Die Eingangsvariablen Xi können auch auf eine Zustandsnummer X abgebildet werden, somit so mit kann Y auch als Funktion von X aufgefasst werden: Y=f(X)

Beispiel Tresor

In einer Bank steht ein Tresor, es gibt einen Filialleiter A und zwei Angestellte B und C. Damit der Tresor geöffnet werden kann, müssen entweder A und B oder A und C aufschließen. Gesucht ist eine digitale Schaltung, die diesen Sachverhalt repräsentiert.

Schritt 1 (Modellbildung)

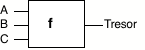Das Problem wird in die Digitaltechnik abgebildet:

Bei vorhandener Person führt eine Personenvariable den Wert 1, ein öffenbarer Tresor wird ebenfalls durch 1 dargestellt, z.B. A = 1: Der Filialleiter ist da. Tresor = 1: der Tresor kann geöffnet werden. Im Modell kann die Schaltung als Funktion Tresor = f(C,B,A) dargestellt werden.

Schritt 2 (Funktionstabelle)

Zn	C	B	A	Q
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	0
7	1	1	1	1

Wie soll sich die Funktion verhalten, wie ist sie definiert?

Das Verhalten kann durch eine Funktionstabelle (Wahrheits- oder Wertetabelle) beschrieben werden.

Die Funktionstabelle liefert den Zusammen-hang zwischen Ein- und Ausgangsgrößen

Anzahl der Kombinationen

Eine Funktionstabelle berücksichtigt alle möglichen Kombinationen der Eingangs-variablen und enthält in den entsprechenden Spalten für die Ausgänge die zugehörigen Werte der Ausgangsvariablen.

n Eingangsgrößen ergeben 2ⁿ mögliche Eingangskombinationen

2ⁿ = 2³ = 8 mögliche Eingangskombinationen

Xen in den Eingangsspalten (Nur TGIT)

Nr.	C	B	A	Y
0,1	0	0	X	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	0
7	1	1	1	1

Nicht immer müssen alle möglichen Zeilen notiert werden. Für den Fall, dass der Wert einer Eingangsvariablen das Verhalten des Ausgangs unabhängig von den anderen Variablen bestimmt, können die entsprechenden Zeilen zusammengefasst werden.

Mengenbegriff: Betrachte Zustände in denen Y=1 als Zielmenge, gesucht f(X)=Y mit f(X)=1 gdw X Elt. in Zielmenge.

Wie kann die Funktion realisiert werden?

Schritt 3 (Synthese einer Funktionsgleichung)

Tresor = (A & B & !C) # (A & !B & C) # (A & B & C)

Schritt 4 (Vereinfachen der Gleichung)

Tresor = A & (B # C)