:TI-BASIS: Die Ampel

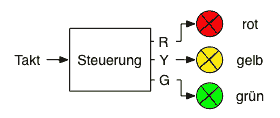
Einfache Ampel-Steuerung mit synchronem Moore-Automat Problem Entwickle eine Steuerung für eine Ampel unter Verwendung eines synchronen Moore-Automaten. Bei jeder steigenden Taktflanke soll ein Ampelbild weitergeschaltet werden:

Blockschaltbild Ampelbilder Ampelbild 0 1 2 3 Rot 0 0 1 1 Gelb 0 1 0 1 Grün 1 0 0 0

Analyse

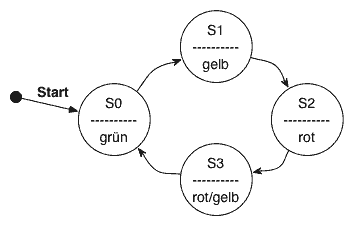
Zustandsdiagramm	Kodierung		neues Blockschaltbild
	English State R Y G S0 0 0 1 S1 0 1 0 S2 1 0 0 S3 1 1 0	Deutsch Zustand Rt Ge Gn Z0 0 0 1 Z1 0 1 0 Z2 1 0 0 Z3 1 1 0

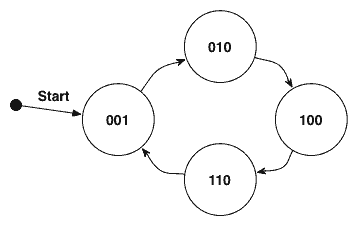
Die Abfolge der Zustände wird im Zustandsdiagramm (engl. State-Diagram) grafisch festgehalten, an die Übergänge muss keine Bedingung geschrieben werden, da bedingungslos nach jeder steigenden Taktflanke der Zustand gewechselt wird. Die Kodierung und Bezeichnung der Zustände wurde hier in englisch getätigt, es ist einfach praktischer..

Design

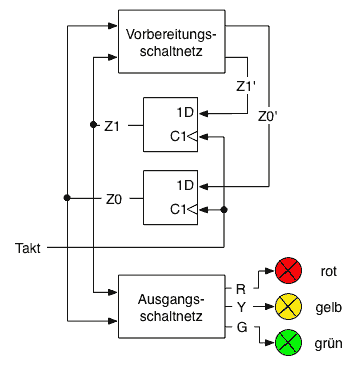
Nun muss eine Entscheidung getroffen werden zwischen Automat mit und ohne Ausgangsschaltnetz. Hier beide Lösungen:

Lösung mit Ausgangsschaltnetz

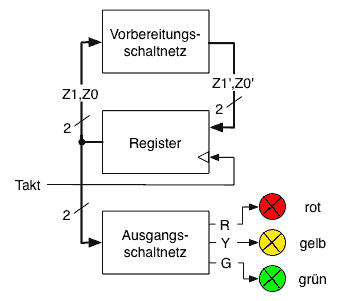
Merken der Zustände in D-Flip-Flops	Zusammenfassen zu Registern

Beschreibung der Funktionen der Schaltnetze in Funktionstabellen (Zustands-Übergangs-Tabelle)

Zustands-Übergangs-Tabelle	Vereinfachung durch Zähler
akt. Zustand next State Output State Z1 Z0 Z1' Z0' R Y G S0 0 0 0 1 0 0 1 S1 0 1 1 0 0 1 0 S2 1 0 1 1 1 0 0 S3 1 1 0 0 1 1 0

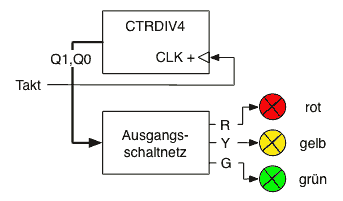
Ausgehend vom aktuellen Zustand wird in der Zustands-Übergangs-Tabelle der Folge-Zustand beschrieben, die Funktion des Vorbereitungs-Schaltnetzes.
Praktischerweise kann auch gleich die Funktion des Ausgangs-Schaltnetzes festgelegt werden. Hier ist die Abfolge der Zustände trivial, es werden einfach die Zustände durchgezählt, somit kann diese Aufgabe von einem Zähler 0..3 übernommen werden.

Lösung ohne Ausgangsschaltnetz

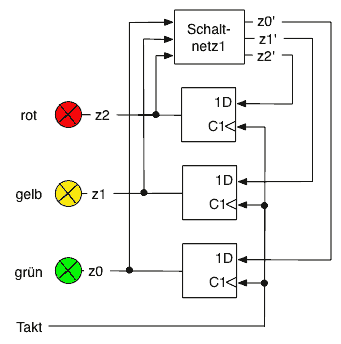
Blockschaltbild	Zustandsdiagramm	Zustands-Übergangs-Tabelle
		akt. Zustand next State State Dual Z2 Z1 Z0 Z2' Z1' Z0' - 0 0 0 0 * * * S0 1 0 0 1 0 1 0 S1 2 0 1 0 1 0 0 - 3 0 1 1 * * * S2 4 1 0 0 1 1 0 - 5 1 0 1 * * * S3 6 1 1 0 0 0 1 - 7 1 1 1 * * *

Hier konnte das Ausgangsschaltnetz eingespart werden zu Lasten eines weiteren D-Flip-Flops. Die Hälfte des Definitonsbereichs des Schaltnetzes sind Don't Care's.

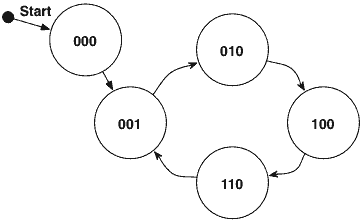
Leider hat die Lösung oben einen Haken: Welchen Zustand haben die D-Flip-Flops nach dem Einschalten der Spannung? Oft wird durch eine Reset-Schaltung dafür gesorgt daß der Startwert Null ist. Nach dem Start wird somit der Zustand 000 angefahren, allerdings ist dafür kein Folgezustand definiert -Problem! Hier nun die richtige Lösung:

Zustandsdiagramm	Zustands-Übergangs-Tabelle
	akt. Zustand next State State Dual Z2 Z1 Z0 Z2' Z1' Z0' Reset 0 0 0 0 0 0 1 S0 1 0 0 1 0 1 0 S1 2 0 1 0 1 0 0 - 3 0 1 1 * * * S2 4 1 0 0 1 1 0 - 5 1 0 1 * * * S3 6 1 1 0 0 0 1 - 7 1 1 1 * * *

Die Ampel bleibt nach einem Reset oder bei Spannungswiederkehr einen Takt dunkel um dann in einen regulären Betriebszustand zu springen.

Aufgabe Ampel-Anlage

Entwickeln Sie eine Ampelsteuerung für eine einfache Fußgängerampel Buch bis S 109 beachten:

• Es gibt einen Takt (Sie sollen einen synchronen Moore-Automaten basteln).
• Die Fußgänger haben einen Wunsch-Knopf.
• Denken Sie über die Use-Cases nach, wie sieht ein typischer Ablauf aus, z.B. Knopf gedrückt, 10 Takte sinnlos warten, 2 Takte Gelb usw.
• Wie viele Zustände benötigt der Automat?

Erstellen Sie ein Blockschaltbild für die Steuerung.

Entwickeln Sie ein Zustandsdiagramm für die Steuerung, zeichnen Sie in die Zustände die Anzeige der Ampeln mit ein z.B.

Entwickeln Sie eine Zustands-Übergangs-Tabelle und Tabellen für die weiteren Schaltnetze Ihre Lösung.

Implementieren und testen Sie ihre Lösung mit Design-Expert.