MezData-Logo

Aufgaben zu gemischten Schaltungen

Einfache gemischte Schaltung

Berechnen Sie alle Ströme und Spannungen!

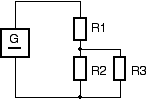
UG = 10V
R1 = 1kΩ
R2 = 1kΩ
R3 = 2kΩ

Lösung

Rges = R2//R3+R1 = 1.66 kΩ

I1 = UG / Rges = 10V / 1.66 kΩ = 6mA

U1 = R1 * I1 = 6V

U2 = U3 = UG - U1 = 4V

I2 = 2/3 I1 = U2 / R2 = 4mA

I3 = 1/3 I1 = U2 / R3 = 2mA

Einfache gemischte Schaltung

Berechnen Sie die Generatorspannung UG!

UG = ?
IR3 = 3mA
R1 = 1kΩ
R2 = 1kΩ
R3 = 2kΩ

Lösung

U2 = U3 = R3 * IR3 = 6V

I1 = I2 + IR3 = U2 / R2 + IR3 = 9mA

U1 = R1 * I1 = 9V

UG = U1 + U2 = 15V

Brückenschaltung

Berechnen Sie die Spannung UAB zwischen den Punkten A und B!
Wie groß kann der Strom durch einen zwischen den Punkten angeschlossenem Widerstand maximal sein?
Begründen Sie Ihre Antwort. Wieviel Strom fließt durch den Generator?

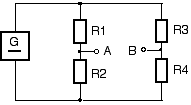
UAB = ?
UG = 10V
R1 = 1kΩ
R2 = 2kΩ
R3 = 2kΩ
R4 = 4kΩ

Lösung

Spannung UAB ist die Spannung zwischen A und B:

UAB = UR2 - UR4, d.h. wenn UR2 > UR4 dann ist UAB positiv

UR2 = UG * R2 / (R1 + R2) = UG * 2/3 = 6,66V

UR4 = UG * R4 / (R3 + R4) = UG * 4/6 = 6,66V

UAB = 0V, somit ist der maximale Strom zwischen den Punkten 0A, denn ohne Spannung kein Strom

RGes = (R1 + R2) // (R3 + R4) = 3kΩ // 6kΩ = (3kΩ * 6kΩ) / (3kΩ + 6kΩ) = 2kΩ

IG = UG / RGes = 10V / 2kΩ = 5mA

Gemischte Schaltung

Berechnen Sie den Gesammtwiderstand der Schaltung, UG = 10V, R1=R2=R3=R4=R5=1kΩ.

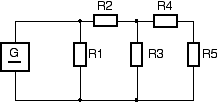
Lösung

Der Trick ist hinten anzufangen:

Rx = R3 // (R4 + R5) = 666Ω

Ry = R2 + Rx = 1,666kΩ

RGes = R1 // Ry = 625Ω

Lampe mit Vorwiderstand

Die Lampe soll mit ihren Nenndaten betrieben werden, berechnen Sie UG!

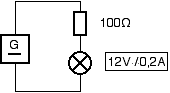
Lösung

Nenndaten bedeuten Spannung an der Lampe: 12V

Strom durch die Lampe: 0,2A

UG = 12V + (100Ω * 0,2A) = 32V

Gleichstromkreis

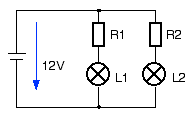
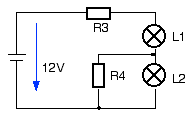
Zwei Glühlampen sollen an einem Akkumulator mit den Nenndaten 12V / 60Ah betrieben werden. Hierzu stehen zwei Schaltungen zur Verfügung:

Schaltung 1 Schaltung 2
Nenndaten der Lampen:
 Lampe L1: 6V / 15W
Lampe L2: 3V / 3W
  1. Welche Ströme fließen in den Lampen L1 und L2 bei den Nenndaten?
  2. Berechnen Sie die Vorwiderstände R1 und R2 für Schaltung 1, damit die Lampen im Nennbetrieb eingesetzt sind.
  3. Welche Widerstände R3 und R4 sind in Schaltung 2 für den Nennbetrieb der Lampen notwendig?
  4. Berechnen Sie jeweils die gesamte Verlustleistung der Widerstände bei beiden Schaltungen
  5. Wie lange kann jede der beiden Schaltungen durch eine Akkumulatorladung betrieben werden? (U=12V)
  6. Welche Folgen ergeben sich für die Lampe L1 in Schaltung 2, wenn die Lampe L2 durchbrennt? (Begründung ohne Rechnung)
Lösung
a. b. c.
P = U / I -> I = P / U

IL1 = 15W / 6V = 2,5A

IL2 = 3W / 3V = 1A

 UR1 = 12V - UL1 = 6V

R1 = UR1 / IL1 = 2,4 Ohm

UR2 = 12V - UL2 = 9V

R2 = UR2 / IR2 = 9 Ohm

 IR3 = IL1 = 2,5A

UR3 = 12V - UL1 - UL2 = 3V

R3 = UR3 / IL1 = 1,2 Ohm

IR4 = IL1 - IL2 = 2,5A - 1A = 1,5A

UR4 = UL2 = 3V

R4 = UL2 / IR4 = 2 Ohm
d. e. f.
PR1 = PL1 = 15 W, wegen UR1 = UL1

PR2 = UR2 * IL2 = 9W

PR3 = UR3 * IL1 = 7,5W

PR4 = UL2 * IR4 = 4,5W

 Q = I * t -> t = Q / I

Schaltung 1: IGes = 2,5A +1A = 3,5A

t1 = 60Ah / 3,5A = 17,1h

Schaltung 2: IGes = IL1 = 2,5A

t2 = 60Ah / 2,5A = 24h

 L1 wird dunkler, weil durch den Wegfall von L2 ihr
Vorwiderstand grösser wird.